題目內容
（請給出正確答案）
[主觀題]
歐氏空間V中的線性變換稱為反稱的，如果對任意，α，β∈V，證明：1)為反稱的充分必要條件是，在一組標
歐氏空間V中的線性變換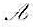
稱為反稱的，如果對任意，α，β∈V，
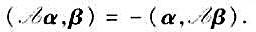證明：
1)
為反稱的充分必要條件是，在一組標準正交基下的矩陣為反稱的;
2)如果V1是反稱線性變換的不變子空間，則
也是。
查看答案
網友您好，
請在下方輸入框內輸入要搜索的題目：
AI搜題
NEW
搜題
更多“歐氏空間V中的線性變換稱為反稱的，如果對任意，α，β∈V，證明：1)為反稱的充分必要條件是，在一組標”相關的問題
第7題
設是P上n維線性空間V的一個線性變換。1)證明：對V上的線性函數f，f仍是V上線性函數;2)定義V*到自
設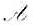
是P上n維線性空間V的一個線性變換。
1)證明：對V上的線性函數f，f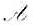仍是V上線性函數;
2)定義V*到自身的映射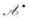
為
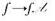。證明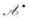：是V*上的線性變換;
3)設ε1，ε2，...，εn是V的一組基，f1，f2，...，fn是它的對偶基，并設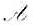在ε1，ε2，...，εn下的矩陣為A，證明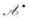：在f1，f2，...，fn下的矩陣為A'。(因此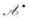稱作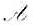的轉置映射。)
第9題
設ε1，ε2，ε3是線性空間V的一組基，f1，f2，f3是它的對偶基，試證α1，α?
設ε1，ε2，ε3是線性空間V的一組基，f1，f2，f3是它的對偶基，
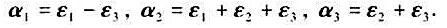
試證α1，α2，α3是V的一組基并求它的對偶基(用f1，f2，f3表出)。
第10題
V=P[x]3，對p(x)=c0+c1x+c2x2∈V定義試證f1，f2，f3都是V上線
V=P[x]3，對p(x)=c0+c1x+c2x2∈V定義
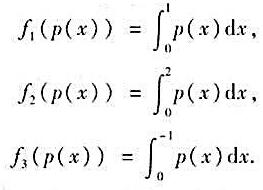
試證f1，f2，f3都是V上線性函數，并找出V的一組基p1(x)，p2(x)，p3(x)使f1，f2，f3是它的對偶基。
第11題
設V是一個n維歐氏空間，它的內積為(α，β)，對V中確定的向量α，定義V上一個函數α*：α*(β)=(α，β)。1)證明：α*是V上線性函數;2)證明：V到V*的映射：α→α*是V到V*的一個同構映射。(在這個同構下，歐氏空間可看成自身的對偶空間。)
熱門考試
全部 >
