問題描述:給定一個無向圖G=(V.E),設(shè)是G的頂點集.對任意,若u∈U且v∈V-U,就稱(u,1)為關(guān)于頂點集U
問題描述:給定一個無向圖G=(V.E),設(shè)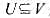 是G的頂點集.對任意
是G的頂點集.對任意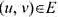 ,若u∈U且v∈V-U,就稱(u,1)為關(guān)于頂點集U的條割邊.頂點集U的所有割邊構(gòu)成圖G的一個割.G的最大割是指G中所含邊數(shù)最多的割.
,若u∈U且v∈V-U,就稱(u,1)為關(guān)于頂點集U的條割邊.頂點集U的所有割邊構(gòu)成圖G的一個割.G的最大割是指G中所含邊數(shù)最多的割.
算法設(shè)計:對于給定的無向圖G,設(shè)計一個優(yōu)先隊列式分支限界法,計算G的最大割.
數(shù)據(jù)輸入:由文件input.txt給出輸入數(shù)據(jù).第1行有2個正整數(shù)n和m,表示給定的圖G有n個頂點和m條邊,頂點編號為1,2,...,n.接下來的m行中,每行有2個正整數(shù)u和y,表示圖G的一條邊(u,v).
結(jié)果輸出:將計算的最大割的邊數(shù)和頂點集U輸出到文件output.txt.文件的第1行是最大割的邊數(shù);第2行是表示頂點集U的向量x(1≤i≤n),x=0表示頂點i不在項點集U中,x=1表示頂點i在頂點集U中.


 搜題
搜題
第1題
設(shè)計一個有效算法求一個有向無環(huán)圖G的最小路徑覆蓋.
[設(shè)V={1,2,...,n},如下構(gòu)造網(wǎng)絡(luò)G1=(V1,E1):
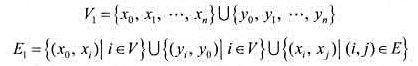
每條邊的容量均為1.求網(wǎng)絡(luò)G1的(x0,y0)最大流.]
算法設(shè)計:對于給定的有向無環(huán)圖G,找出G的一個最小路徑覆蓋.
數(shù)據(jù)輸入:由文件input.txt提供輸入數(shù)據(jù).文件第1行有2個正整數(shù)n和m.n是給定有向無環(huán)圖G的頂點數(shù),m是G的邊數(shù).接下來的m行,每行有2個正整數(shù)i和j,表示一條有向邊(i,j).
結(jié)果輸出:將最小路徑覆蓋輸出到文件output.txt.從第1行開始,每行輸出一條路徑.文件的最后一行是最少路徑數(shù).

第2題
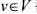 都有權(quán)值w(v).如果
都有權(quán)值w(v).如果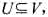 ,且對任意(u,V)∈E有u∈U或v∈U,就稱U為圖G的一個頂點覆蓋.G的最小權(quán)頂點覆蓋是指G中所含頂點權(quán)之和最小的頂點覆蓋.
,且對任意(u,V)∈E有u∈U或v∈U,就稱U為圖G的一個頂點覆蓋.G的最小權(quán)頂點覆蓋是指G中所含頂點權(quán)之和最小的頂點覆蓋.算法設(shè)計:對于給定的無向圖G,設(shè)計一個優(yōu)先隊列式分支限界法,計算G的最小權(quán)頂點覆蓋.
數(shù)據(jù)輸入:由文件input.txt給出輸入數(shù)據(jù).第1行有2個正整數(shù)n和m,表示給定的圖G有n個頂點和m條邊,頂點編號為1,2,...,n.第2行有n個正整數(shù)表示n個頂點的權(quán).接下來的m行中,每行有2個正整數(shù)u和v,表示圖G的一條邊(u,v).
結(jié)果輸出:將計算的最小權(quán)頂點覆蓋的頂點權(quán)值和以及最優(yōu)解輸出到文件output.txt.文件的第1行是最小權(quán)頂點覆蓋頂點權(quán)之和;第2行是最優(yōu)解xi(1≤i≤n),xi=0表示頂點i不在最小權(quán)頂點覆蓋中,xi=1表示頂點i在最小權(quán)頂點覆蓋中.

第3題
第5題
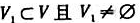 ,均有P(G-V1)≤|V1|,則G是哈密頓圖。以上結(jié)論成立嗎?為什么?
,均有P(G-V1)≤|V1|,則G是哈密頓圖。以上結(jié)論成立嗎?為什么?
第6題
A.G’為G的子圖
B.G’為G的連通分量
C.G’為G的極小連通子圖且V=V’
D.G’是G的一個無環(huán)子圖
第7題
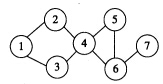
第8題
A.G’是G的子圖
B.G’是G的連通分量
C.G’是G的極小連通子圖且V=V’
D.G’是G的一個無環(huán)子圖
第9題
A.G是G的子圖
B.G是G的連通分量
C.G是G的無環(huán)子圖
D.G是G的極小連通子圖,且V"=V
第10題
A.G'為G的子圖
B.G'為G的連通分量
C.G'為G的極小連通子圖且V'=V
D.G'是G的一個無環(huán)子圖
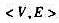 ,且對任意結(jié)點v∈V,有d(v)≥2。試證,G至少有一基本圈。
,且對任意結(jié)點v∈V,有d(v)≥2。試證,G至少有一基本圈。