對于一維自由粒子(a)設波函數為,試用算符對運算,驗證說明動量本征態量能量本征態,能量本征值為
對于一維自由粒子
(a)設波函數為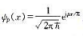 ,試用
,試用 算符
算符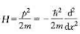 對
對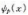 運算,驗證
運算,驗證
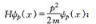
說明動量本征態量能量本征態 ,能量本征值為
,能量本征值為
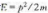
(b)設粒子在初始(t=0)時刻,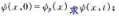
(c)設波函數為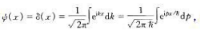 可以看成無窮多個平面波
可以看成無窮多個平面波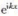 的疊加,即無窮多個動量本征態
的疊加,即無窮多個動量本征態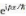 的疊加,試問
的疊加,試問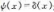 是否是能量本征態?
是否是能量本征態?
(d)設粒子在t=0時刻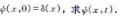
 搜題
搜題
第2題
自由運動,波函數滿足周期性邊界條件ψ(x)=ψ(x+L).試寫出動量和Hamilton量的共同本征函數(不考慮自旋);
(b)加上微擾H'=εcosqx,其中Lq=4πN(N為大的正整數).試就電子動量|p|=qh/2的情況求能級和定態波函數,準確到ε量級;
(c)再計算情況(b)的能級修正,至ε2量級;
(d)對于|p|接近(但不等于)qh/2的情況,重復(b)和(c)的能級計算.
第3題
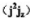 的本征態,記為
的本征態,記為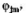 能級與m無關,為
能級與m無關,為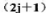 重簡并,設有兩個全同粒子處于此能級上。證明:(a)交換對稱態和反對稱態的數目分別為(j+1) (2j+1)和j (2j+1),(b)無論粒子是Bose子或Fermi子,體系的角動量J必為偶數。
重簡并,設有兩個全同粒子處于此能級上。證明:(a)交換對稱態和反對稱態的數目分別為(j+1) (2j+1)和j (2j+1),(b)無論粒子是Bose子或Fermi子,體系的角動量J必為偶數。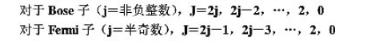
第4題
一維諧振子的Hamilton量為
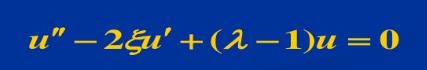 ,x∈(-∞,∞).
,x∈(-∞,∞).
在坐標表象中,它的能量本征態波函數為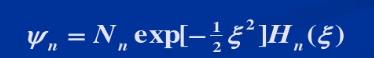 ,這里Nn是歸一化系數,Hn為Hermite多項式.試在動量表象中求出它的能量本征值和相應的波函數.
,這里Nn是歸一化系數,Hn為Hermite多項式.試在動量表象中求出它的能量本征值和相應的波函數.
第5題
ψ(r,θ,φ,sz)=αYl0(θ,φ)R(r) (1)
求總角動量j2,jz的可能測值及相應概率(取h=1).
第8題
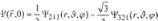 狀態,其中
狀態,其中 是氫原子哈密頓算符的正交歸一化本征波函數。
是氫原子哈密頓算符的正交歸一化本征波函數。求:(1) t=0時刻,體系能量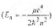 的平均值。
的平均值。
(2) t=0時刻,體系角動量平方L2的平均值。
(3) t=0時刻,體系角動量x分量Lx的平均值。
(4) 時刻,體系所處的狀態
時刻,體系所處的狀態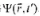 。
。
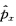 的本征值。
的本征值。